3D 列印至今已是非常普遍使用的一項技術,不過在這項技術之後還有所謂的 4D 列印。所謂的 4D 列印是藉由一種特殊的平面結構,透過濕度或溫度等環境變化,使其變形成不同的形狀。而現在 MIT 麻省理工學院的科學團隊打造出了一種平面結構,得以用其變化出以往 4D 列印技術所無法達成的複雜結構,例如人臉。並且將研究結果發表於美國國家科學院院刊上。
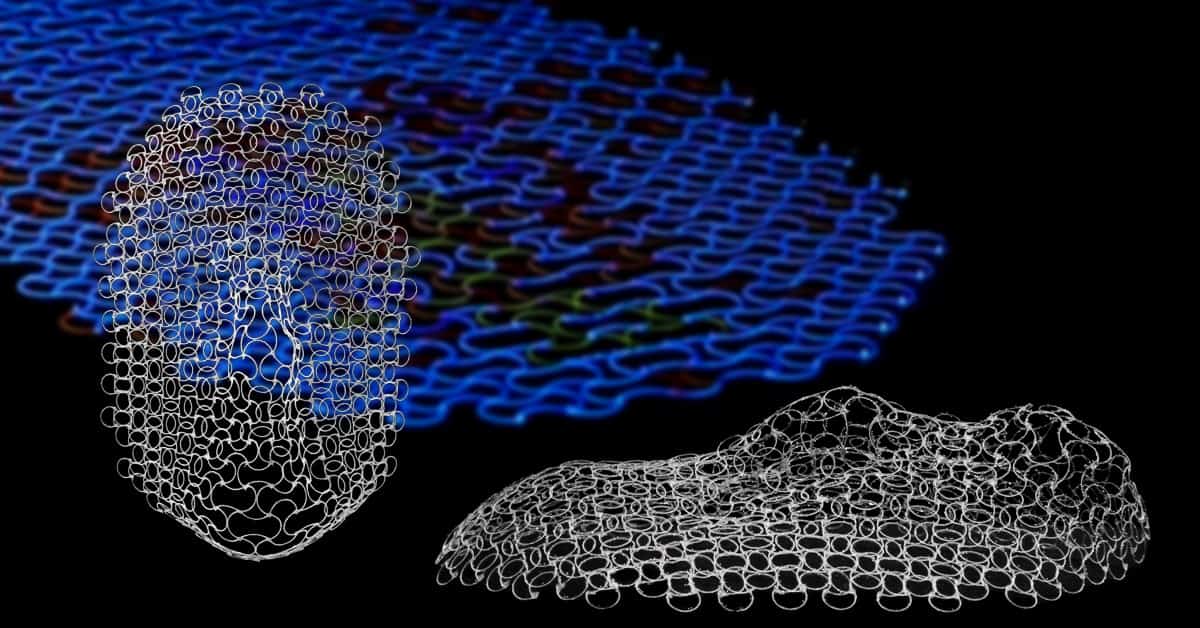
過去的 4D 列印技術雖然也可以將平面結構變成其他結構,但往往結構都過於簡單,實用性也較低。而麻省理工的機械工程師 Wim van Rees 則設計出了一種理論方法,能夠將一個薄型平板變形成諸多複雜的形狀,像是球狀、圓頂,甚至是人臉。可是他自然得要面對一個難以克服的問題——絕妙定理。
在 1828 年,德國物理學家高斯發現了絕妙定理,絕妙定理說明物體表面的曲率並不會因為外力彎折而產生改變。對於 4D 列印而言,van Rees 表示這就像是要將一張紙包裹住一顆球,無論你怎麼樣包覆,都勢必要把紙張的邊弄皺,這是因為紙張本身為零高斯曲率,球卻是雙曲率,所以紙張得要經過拉伸或收縮才能夠完整包覆好一顆球。然而 4D 列印的表面規則卻是不能拉伸、收縮或撕裂。

為了克服這個問題,van Rees 與其同事決定使用網狀格子構造,他們透過橡膠材料製作出格子,使這些格子會因為溫度升高而膨脹,而格子中間的空隙就能讓材料適應表面部分的大幅度變化。之後該團隊設計出了一種算法,將格子的架構變形成正確的形狀,並成功將一平面結構變形成高斯的臉部結構。
除此之外,該團隊還製作出了含有導電液態金屬的格子,可以變形成主動式天線,其共振頻率能夠隨著材料的變形而產生改變。
這種變形材料有朝一日或能應用在諸多領域,例如用它來開發出可以自行架設、收折的帳篷;可變型的望遠鏡頭、支架、人造組織支架,或是軟體機器人等等。

